Baseline Algorithm Definition

In the following sections, the Level-2 sea-ice drift algorithm is further described. It consists in those steps:

• resampling og Level-1b data;

• selection of tracking locations and preliminary screening;

• block-based maximisation of the correlation metric via the CMCC;

• filtering and correction step;

• assign status flags and per-vector uncertainties.

Sea-ice motion tracking is performed at the intersection of two swaths. The motion tracking itself requires that the brightness temperature imagery is first resampled to a common grid. This makes the level-2 sea-ice drift product quite different from other level-2 products in that:

1. the Level-1b data must be remapped to a common (polar) grid as part of the processing, e.g. an EASE2 grid;

2. as a consequence, the Level-2 sea-ice drift product is presented on an EASE2 grid (not in a swath projection);

3. the algorithm operates not with one, but with at least two Level-1b files as input;

4. for each incoming Level-1b file, one can generate more than one Level-2 sea-ice drift product (consider the swath intersection with the most recent Level-1b swath, the one before, etc…)

CIMR Level-1b re-sampling approach

The re-sampling approach for resampling CIMR Level-1b Ku and Ka band imagery is not defined at this stage. From experience with sea-ice motion tracking from other passive microwave mission, the Level-1b re-sampling approach does not have a large influence on the results. At this stage, the following characteristics are expected from the re-sampling:

1. Remap incoming Level-1b files on two EASE2 polar grids (one covering northern hemisphere, the other covering the southern hemisphere);

2. Remap 4 imagery channels (Ku-V, Ku-H, Ka-V, Ka-H);

3. Remap the forward and backward scans separately;

4. Aim at a grid spacing close to 5 km (TBC).

Table 4 defines four grids, two for the northern hemisphere, two for the southern hemisphere. nx (ny) is the number of grid cells in x (y) dimension, Ax (Ay) is the grid spacing, and Cx (Cy) is the coordinate of the upper-left corner of the upper-left cell in the grid. Grids (n,s)h_ease2-005 have 5 km grid spacing and are candidate target grids on which to remap the Level-1b imagery. Grids (n,s)h_ease2-250 have 25 km grid spacing and are candidate grids for the resulting Level-2 sea-ice drift product. By construction, the center of the cells of the two ‘250’ grids fall exactly at the center of one every five grid cells of the ‘005’ grids. This ensures that drift vectors (at every grid cell of the ‘250’ grids) use image blocks (from the ‘005’ grids) that are perfectly aligned.

Table 4 Definition of EASE2 grids used in the Level-2 sea-ice drift processing (TBC)

Id	nx	ny	Ax [km]	Ay [km]	Cx [km]	Cy [km]
nh_ease2-250, sh_ease2-250	432	432	25.0	25.0	-5400.0	-5400.0
nh_ease2-005, sh_ease2-005	2160	2160	5.0	5.0	-5400.0	-5400.0

Such a ‘1-every-5’ construct is not a requirement of the sea-ice drift algorithm, but a simplification used in many motion extraction algorithms. Other alternatives are to grid the Level-1b data with 4 km spacing and consider a ‘1-every-6’ ratio (Level-2 grid spacing at 24 km) or keep a ‘1-every-5’ ratio (Level-2 grid spacing at 20 km).

The remaining of the algorithm description does not depend on this choice, which can easily be changed in the course of the product development.

Each incoming Level-1b file thus results in 16 gridded fields of brightness temperature: 2 hemispheres x 2 scans x 4 bands. These can be written in two L1C-like netCDF files (1 per hemisphere) or directly entered in the motion tracking algorithm. They must be written to netCDF files at one point so that they are available for sea-ice drift processing when the next Level-1b swath file arrives.

Algorithm Assumptions and Simplifications

All block-based motion have similar assumptions and simplifications. They assume that each pixel in a block moves at a constant rate from one image to the next: what is retrieved are the dx and dy components of the motion vector. In case of rotational motion within the area of the image block, the retrieved components will be those representing most faithfully the change in intensity between the two images, but the rotation rate is not measured. By the same token, if deformation (convergence / divergence / shear) occurs within the area of the image blocks, this will not be detected. Rotation and deformation betwen image blocks (between neighbouring pixels) can of course be detected.

To detect and possibly correct “rogue” vectors in the motion field, we have to assume that the motion field is spatially coherent in a neighbourhood. This is because we detect anomalous motion vectors by their distance to the local average motion. One must be careful with this assumption as to not artificially smooth the motion fields and remove actual diverging / converging motion.

Level-2 end to end algorithm functional flow diagram

Fig. 3 shows the flow diagram for the CIMR Level-2 sea-ice drift algorithm. Note the structure in two chains: preprocessing of the image, and sea-ice motion tracking per se.

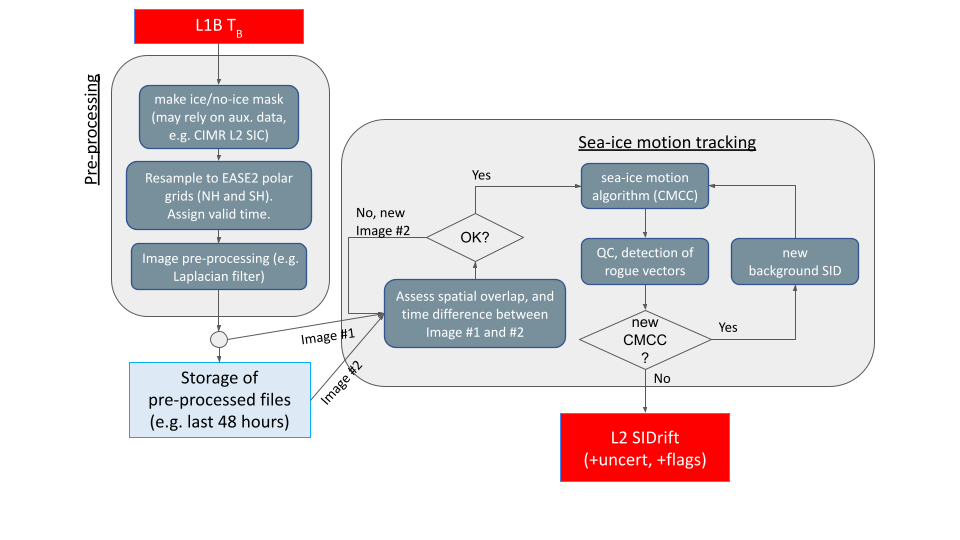
Fig. 3 End-to-end algorithm flow diagram of the CIMR Level-2 sea-ice drift algorithm

Functional description of each Algorithm step

Pre-processing

Prepare ice/ocean/land mask

The Level-2 sea-ice drift algorithm shall only be applied over sea-ice portions of the image. We thus need to prepare an ice/ocean mask as well as a land-mask to only process over sea ice.

Input data

The latitude and longitude of the image grids nh_ease2-005 and sh_ease2-005.

Output data

A 2D field of ice/no-ice/land on the image grids.

Auxiliary data

A source of sea-ice concentration (can be from CIMR Level-2 Sea Ice Concentration product, or Level-2 Integrated-Retrieval product).

Remap Level-1b brightness temperatures to the EASE2 image grids

The Level-1b data (brightness temperature at Ku-V, Ku-H, Ka-V, Ka-H) are remapped onto the EASE2 image grids nh_ease2-005 and sh_ease2-005. The forward and backward scans are remapped independently.

A valid time is associated to the remapped imagery. It can be defined as the mean time of all the Level-1b samples remapped onto the image grid or the time of the observation closest to the (north or south pole). The exact definition is not critical, neither is the accuracy, so that a single valid time is associated to all 8 remapped imagery bands in the northern hemisphere, and a single (different) time to the 8 remapped imagery bands i nthe southern hemisphere.

Mathematical description

Remapping is the process of computing the Level-1b brightness temperature onto a regular Earth-based grid. The values in the image grid can generally be described as a weighted sum of the values in the Level-1b swath projection. The mathematical description is TBD and will depend on the selected remapping strategy (TBD for v2 ATBD).

Input data

The latitude and longitude of the image grids nh_ease2-005 and sh_ease2-005.

The Level-1b brightness temperatures of all samples in the input Level-1b file, splitted in a forward and a backward scan.

Output data

16 2D field of brightness temperature on the image grids (2 grids x 2 scans x 4 channels).

Ancillary data

The latitude and longitude of all the Level-1b samples.

Image preprocessing (Laplacian filter)

The remapped brightness temperatures are not used direclty as input to the sea-ice motion tracking step. Instead, a filter is first applied to the remapped imagery to enhance and stabilize intensity patterns.

At the end of the step, the laplacian processed imagery are saved to disk, e.g. in netCDF files (two separated files for the two hemispheres).

Mathematical description

A common filter, used by Girard-Ardhuin and Ezraty [2012] and Lavergne et al. [2010], is the Laplace filter, that is based on computing the second derivatives of the image intensity.

(1)\[\begin{split} \begin{split} \mathcal{L}[i,j] &= \frac{1}{N^{+}} \sum_{n=i-1}^{i+1} \sum_{m=j-1}^{j+1} \delta_{\textrm{na}}(n,m) \delta_{\textrm{ice}}(n,m) \delta_1^{i,j}(n,m) \mathcal{I}[n,m] \\ &- \frac{1}{N^{-}} \sum_{n=i-2}^{i+2} \sum_{m=j-2}^{j+2} \delta_{\textrm{na}}(n,m) \delta_{\textrm{ice}}(n,m) \delta_2^{i,j}(n,m) \mathcal{I}[n,m] \end{split} \end{split}\]

with

(2)\[\begin{split} \begin{aligned} \delta_k^{i,j}(n,m) & = & \left\{ \begin{array}{ll} 1 & \mbox{if $|i-n| = k$ or $|j-m| = k$};\\ \nonumber 0 & \mbox{otherwise}.\end{array} \right. \\ \nonumber N^{+} &=& \sum_{n=i-1}^{i+1} \sum_{m=j-1}^{j+1} \delta_{\textrm{na}}(n,m) \delta_{\textrm{ice}}(n,m) \delta_1^{i,j}(n,m) \leq 8 \\ \nonumber N^{-} &=& \sum_{n=i-2}^{i+2} \sum_{m=j-2}^{j+2} \delta_{\textrm{na}}(n,m) \delta_{\textrm{ice}}(n,m) \delta_2^{i,j}(n,m) \leq 16 \nonumber \end{aligned} \end{split}\]

In Eq. (1) and (2), \(\delta_{\textrm{na}}(n,m)\) has value \(0\) if \(\mathcal{I}[n,m]\) is non available (a missing value in the swath, or missing values outside the coverage of the swath) and \(\delta_{\textrm{ice}}(n,m)\) is \(1\) only over ice pixels, as specified by the ice/water/land mask. It means that only valid, sea ice pixels enter the Laplacian field in order to limit spurious features along the ice edge, coastline or at the border of the swath coverage.

\(\mathcal{L}[i,j]\) is only computed if the centre cell \([i,j]\) is itself over sea ice, \(\delta_{\textrm{ice}}(i,j)=1\).

In the event when \(N^{+} < 5\) or \(N^{-} < 9\), not enough pixels are available for computing \(\mathcal{L}\) and a missing value is stored at grid cell \([i,j]\).

Input data

The remapped brightness temperatures on the image grids (16 2D fields).

Output data

16 2D field of laplacian-filtered brightness temperature on the image grids.

Ancillary data

The ice/water/land mask on the image grids.

Sea-ice motion tracking

To compute sea-ice drift vectors require two images. A start and an end image. In the near-real-time Level-2 processing context, the end image is the (laplacian filtered) remapped imagery from the input Level-1b file. Start images are taken from a running pool of remapped imagery from the previous runs of the sea-ice drift algorithm. In principle, many start images can be selected and run into the sea-ice motion tracking against the end image. The difference between the valid time of the start and end imagery determines the drift duration (aka time span) of the Level-2 drift vectors.

At minimum (and in priority), the Level-2 sea-ice drift algorithm should be applied once with a start image with valid time approximately 24 hours before the valid time of the end image. This results in 24 hours drift vectors. Ideally, the sea-ice motion tracking algorithm described below is applied for several (start, end) image pair to obtain a good temporal sampling of the sea-ice motion (e.g. 24 hours, 18 hours, 12 hours, 6 hours, etc…). At max, the sea-ice motion tracking algorithm would be applied with all (start, end) image pairs for which the valid time of the start image is less or equal to 24 hours from the valid time of the end image. Each (start, end) image pair will correspond to different area of intersect between the two swaths, and thus to different numbers of resulting sea-ice drift vectors. Pairs with too limited overlaps could be discarded up-front to favour processing pairs with a large overlap. Because swath-to-swath motion tracking is very sensitive to (systematic) geolocation errors [Lavergne et al., 2021] it might be preferrable to not process some pairs (e.g. ascending vs descending) that would have larger uncertainties.

A hard limit is that the processing of all the image pairs must happen before the next input Level-1b input file is available for processing. Parallel computing strategy will help reduce the total processing time (since each image pair can be processed independently from each others). A schedulding strategy must be designed to affort the maximum number of image pairs before it causes a problem for product latency.

At this stage it is TBD if each (start, end) image pairs results in individual Level-2 product files (better for the latency) or if all the sea-ice drift vectors (with different time spans) are concatenated in a single Level-2 product file.

In any case, the description below is for a single (start, end) image pair, and for each image grid (nh and sh) separately.

Select grid locations where to apply the CMCC algorithm

The CMCC can only be applied where the two swaths (start and end images) overlap over sea ice. A first step in the processing is thus to go through all the positions in the (n,s)h_ease2-250 grid and test if there is sufficient overlap between the two images, and if the overlap is over sea ice.

Logical description

For each grid position in the Level-2 product grid, the following tests are performed.

Masking of land pixel (step 1)

• Blocks whose centre pixel is over land are discarded;

Masking of pixels with not enough sea ice (step 2)

• The start and end blocks of the two ice/water/land masks are loaded. Discard the grid locations whose start and end blocks are not entirely over ice.

Masking of pixels with missing data (step 3)

• The start and end blocks of the Laplacian images are loaded. Discard the grid locations whose blocks hold missing data.

The positions that are not discarded after those three steps are passed to the next processing step (CMCC).

Input data

The two (start and end) ice/ocean/land masks on the image grid (n,s)h_ease2-005.

The two (start and end) laplacian-filtered brightness temperature maps on the image grid (n,s)h_ease2-005.

The diameter of the sub-image (aka image block) to be used in the CMCC, in number of pixels.

The definition of the Level-2 product grid (n,s)h_ease2-025.

Output data

A 2D field of status flags recording the status at the end of this selection step (in particular recording where and why CMCC will not be attempted).

Run the CMCC algorithm

The CMCC is the core sea-ice motion algorithm

Mathematical description

We note \(\mathcal{L}_0(x,y)[i]\) the \(i^{th}\) pixel of the start sub-image centred at point \((x,y)\), extracted from the \(\mathcal{L}_0\) image. \((x,y)\) are the coordinates expressed in the underpinning EASE2 projection (units km).

The total number of pixels \(N\) in a sub-image depends on the diameter of the sub-image (input parameter).

The mean and standard deviation values for a given sub-image are:

\[\begin{split} \begin{aligned} \langle \mathcal{L}_0(x,y) \rangle & = & \frac{1}{N} \sum_{i=1}^{N} \mathcal{L}_0(x,y)[i] \nonumber \\ \sigma ( \mathcal{L}_0(x,y) ) & = & \sqrt{\langle \mathcal{L}^2_0(x,y) \rangle - \langle \mathcal{L}_0(x,y) \rangle^2} \nonumber \end{aligned} \end{split}\]

Similar values can be computed for a end sub-image centred at \((u,v)\): \(\langle \mathcal{L}_1(u,v) \rangle\) and \(\sigma ( \mathcal{L}_1(u,v) )\).

The match between a start and a stop sub-image is evaluated via the correlation metric:

(3)\[ \rho(x,y,\delta_x,\delta_y) = \frac{ \sum_{i=1}^{N} (\mathcal{L}_0(x,y)[i]-\langle \mathcal{L}_0(x,y) \rangle) (\mathcal{L}_1(x+\delta_x,y+\delta_y)[i]-\langle \mathcal{L}_1(x+\delta_x,y+\delta_y) \rangle) }{\sigma ( \mathcal{L}_0(x,y) ) \sigma ( \mathcal{L}_1(x+\delta_x,y+\delta_y) )} \]

By construction, \(\rho(x,y,\delta_x,\delta_y)\) takes values between \(-1\) and \(+1\). High values indicate a good match between the sub-images. This is further interpreted as having found the offsets \(\delta_x = u - x\) and \(\delta_y = v - y\) which best explain the local change in intensity between the two sub-images. \((\delta_x,\delta_y)\) is the drift vector.

Pixels of the candidate block \(\mathcal{L}_1(x+\delta_x,y+\delta_y)\) are computed from bi-linear interpolations of the pixels of \(\mathcal{L}_1\). For example, \(\mathcal{L}_1(u,v)[i]\) is given by:

(4)\[\begin{split} \begin{split} \mathcal{L}_1(u,v)[i] & = (1 - \epsilon_{u}) \times (1 - \epsilon_{v}) \times \mathcal{L}_1(\bar{u},\bar{v})[i] \\ &+ (1 - \epsilon_{u}) \times \epsilon_{v} \times \mathcal{L}_1(\bar{u},\bar{v}+s_{v})[i] \\ &+ \epsilon_{u} \times (1 - \epsilon_{v}) \times \mathcal{L}_1(\bar{u}+s_{u},\bar{v})[i] \\ &+ \epsilon_{u} \times \epsilon_{v} \times \mathcal{L}_1(\bar{u}+s_{u},\bar{v}+s_{v})[i] \end{split} \end{split}\]

where

\[\begin{split} \begin{aligned} \bar{t} & = & \operatorname{Trunc}(t) \\ \epsilon_t & = & |t - \bar{t}| \\ s_t & = & \frac{t}{|t|} \end{aligned} \end{split}\]

For example, for \(t=-2.8\), \(\bar{t}=-2\), \(\epsilon_t=0.8\) and \(s_t=-1\). Eq. (4) permits computing virtual sub-images at continuously varying centre points \((u,v)\) and thus building a continuous optimisation framework to the estimation of motion vectors from a pair of images.

Finding the motion vector \((\delta_x,\delta_y)\) at position \((x,y)\) can be expressed as the following maximisation problem:

(5)\[ \max_{(x,y)\in\mathcal{D}} \rho(x,y,\delta_x,\delta_y) \]

which is solved at all grid positions where the motion vector is searched for (see previous step). Each optimisation is conducted independently from the others. \(\mathcal{D}\) is a validity domain for \((\delta_x,\delta_y)\). Eq. (5) thus defines a two dimensional optimisation problem with domain constraint.

Eq. (5) is valid for one pair of images. In the CIMR sea-ice drift algorithm, we however envision not one pair of (start, end) images but 16 pairs (fwd-fwd, fwd-bck, bck-fwd, and fwd-bck) for each of Ku-V, Ku-H, Ka-V, and Ka-H considering the foward and backward scans as separate images. Following Lavergne et al. [2010] we implement an inplicit merging of the information content of the 16 imaging channels by maximizing a sum of cross-correlation functions:

(6)\[ \max_{(x,y)\in\mathcal{D}} \frac{1}{N_{ch}} \sum_{c=1}^{c=N_{ch}} \rho^{c}(x,y,\delta_x,\delta_y) \]

where \(N_{ch}\) is the number of channels (\(N_{ch} = 16\)).

Eq. (6) is solved by the Nelder Mead algorithm [Nelder and Mead, 1968]. This algorithm is chosen since it is simple to implement and does not require computing the gradients of the function to be minimized. It furthermore has good convergence and computational properties in problems with low dimensionality [Lagarias et al., 1998].

Starting points for the optimisation are sampled on a length-angle regular grid around point \((0,0)\) as on Fig. 4.

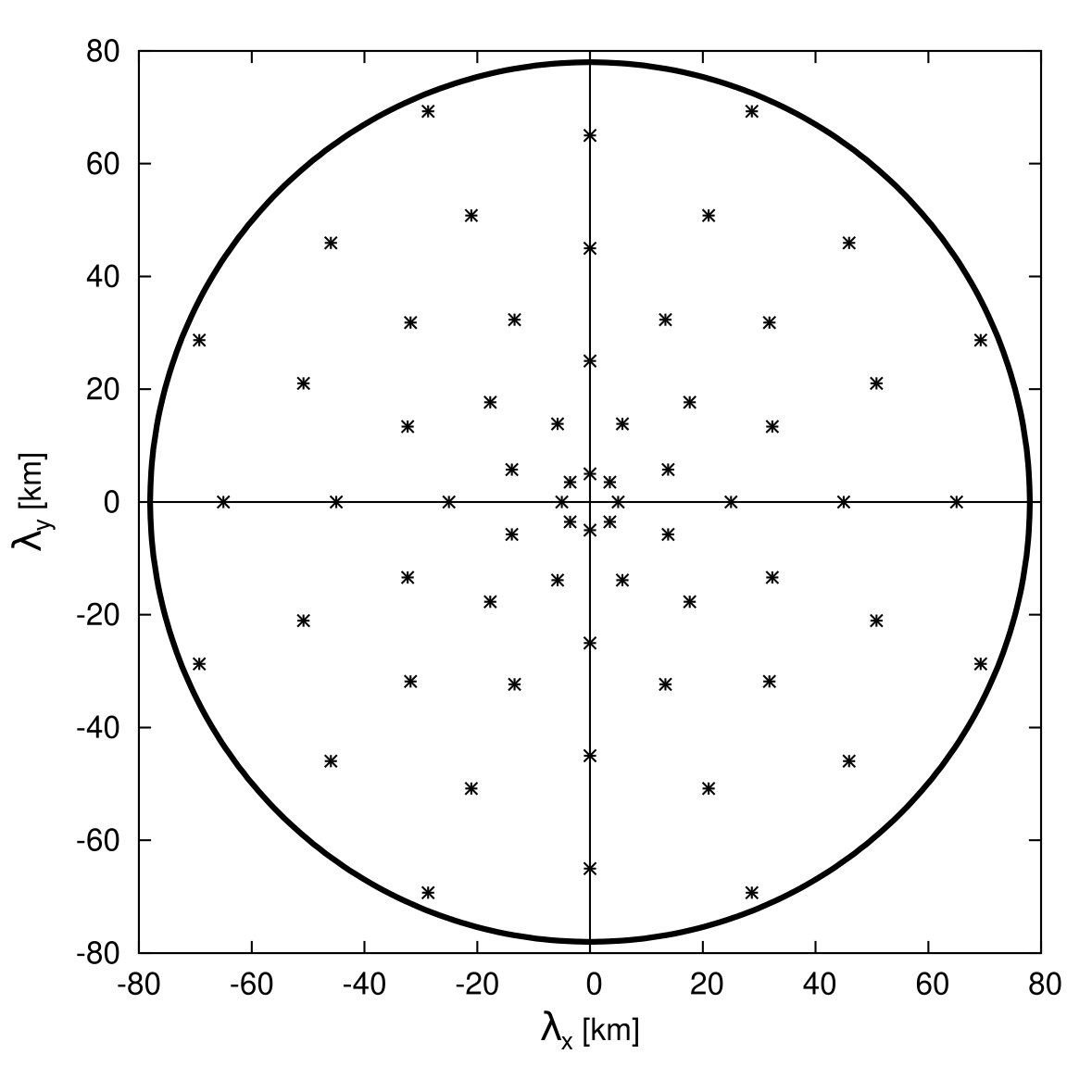
Fig. 4 Initialization points for the Nelder-Mead algorithm, chosen on a regular length-angle grid aroung point \((0,0)\).

The length increment is set to \(10\)km and the angular increment to \(45^{\circ}\). The circle has radius \(\mathbf{L}\), the maximum drift distance defining \(\mathcal{D}\).

\(\rho(x,y,\delta_x,\delta_y)\) is computed at each of those points and the best 3 vertexes are kept for initialising the Nelder-Mead optimisation.

Termination and convergence is tested upon via a relative difference of function values at the current best and worst vertexes, \(f_b\) and \(f_w\). Specifically, the algorithm is said to have converged if and only if \(| f_b - f_w | < (f_b + f_w) \times \tau + \epsilon\), with \(\tau\) and \(\epsilon\) small and positive floating point values. As a safeguard, the maximum number of iterations is set to 1000.

In Eq. (6) \(\mathcal{D}\) is a disc shaped domain expressing the a-priori knowledge we bring to the optimisation problem. Its purpose is to limit the search area for the solution vector during the optimisation process. It is defined by a centre point \((x_c,y_c)\) and radius \(\mathbf{L}\).

(7)\[ (\delta_x,\delta_y) \in \mathcal{D}_{x_c,y_c} \Leftrightarrow d(x_c,y_c;\delta_x,\delta_y) < \mathbf{L} \]

In Eq. (7), \(d(x_c,y_c;\delta_x,\delta_y)\) is the distance (great circle) between the centre point of \(\mathcal{D}\) and the tip of the drift vector \((\delta_x,\delta_y)\). \((x_c,y_c)\) represents our best a-priori knowledge at the time of performing the optimisation. It is initially set to \((0,0)\).

Eq. (7) cannot be used as is in the optimisation routine since it leads to abrupt and non-linear behaviour. \(\mathcal{D}\) is instead implemented as a soft constraint based on a mono-dimensional sigmoid function \(W(d)\):

(8)\[ W(d) = \frac{1}{1 + e^{k(d - \mathbf{L})}} \]

In Eq. (8), \(k\) is a parameter controlling the steepness of the sigmoid around the cut-off value \(\mathbf{L}\). By construction, \(W(\mathbf{L}) = 0.5\). By using a large enough value for \(k\), the \(W\) can be made arbitrarily close to the Heaviside step function, yet remaining smooth and continuous.

Eq. (9) illustrate how the penalty is applied to the correlation function \(\rho^c(x,y,\delta_x,\delta_y)\) (Eq. (6)).

(9)\[ \rho^c_D(x,y,\delta_x,\delta_y) = (\rho^c(x,y,\delta_x,\delta_y) + 1) \times W(d(x_c,y_c;\delta_x,\delta_y)) - 1 \]

Fig. 5 plots a mono-dimensional example of applying a sigmoid penalty function to a synthetic correlation function. Evaluations for \(x\) lower than L are dominated by the correlation value \(\rho(x)\) while those occurring outside the domain (\(x\) larger than \(L\)) return very bad scores, that is close to \(-1\).

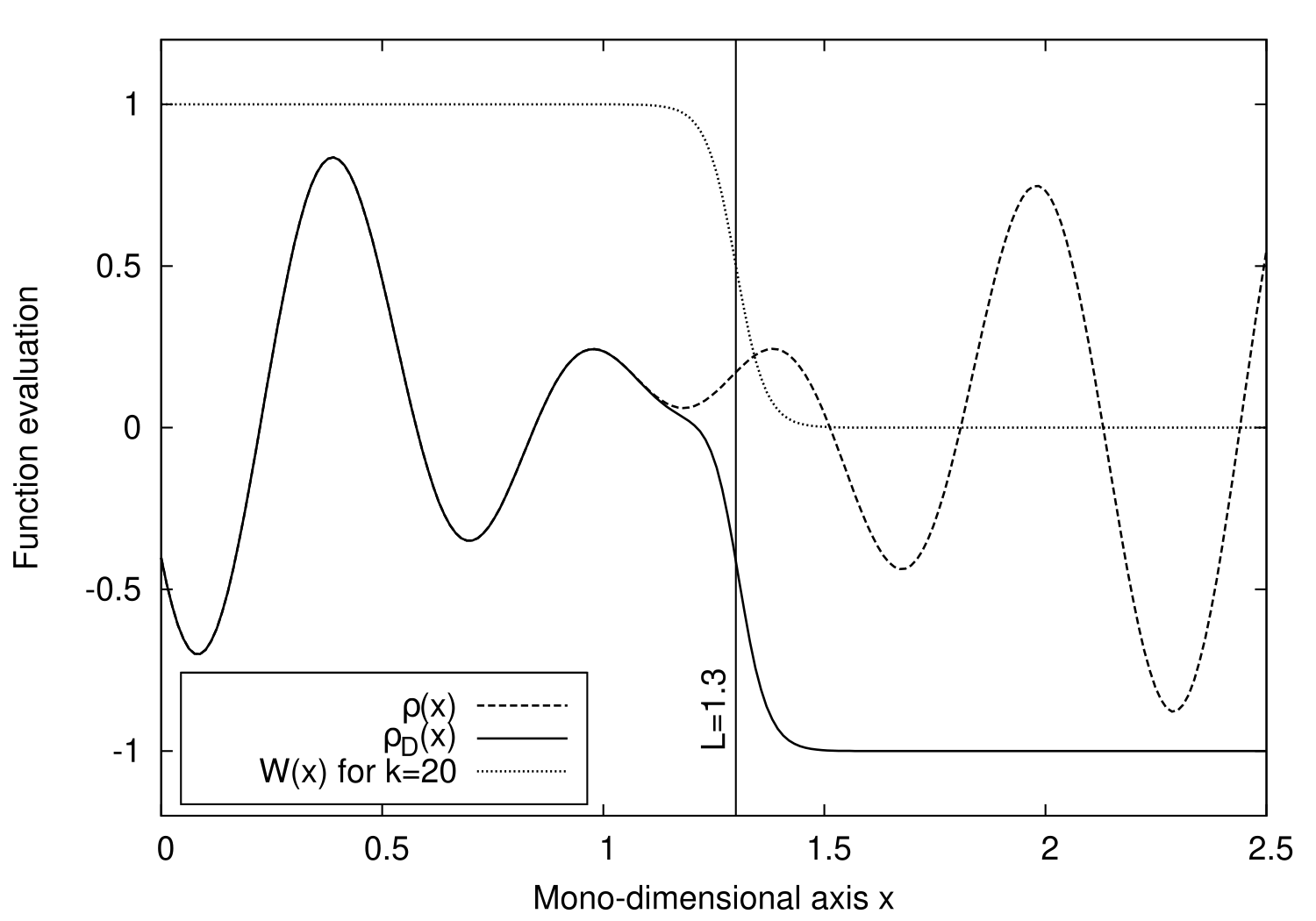
Fig. 5 Example soft constraint implemented with a sigmoid penalisation function \(W\) and its application on a synthetic, mono-dimensional correlation signal \(\rho\). Here, the \(\mathbf{L}\) parameter is \(1.3\) and \(k\) is \(20\).}

In Eq. (9), \(\rho_D\) is the penalised correlation function. Finding the maximum of \(\rho_D\) is taken as a proxy for solving the original, constrained, optimisation problem of Eq. (6). \(\rho_D\) is the function entering the Nelder-Mead algorithm instead of \(\rho\).

It is customary to compute \(\mathbf{L}\) as a maximum expected speed \(v_{max}\), multiplied by the time separation between the valid times of the two images \(\mathbf{T}_1\) - \(\mathbf{T}_0\). \(\mathbf{L}\) is thus the maximum expected straight-line distance that can be covered in the given time.

Input data

The diameter of the sub-image (aka image block) to be used in the CMCC, in number of pixels.

The maximum allowed drift speed \(v_{max}\) (to define \(\mathbf{L}\)) and \mathcal{D}).

The 8 imagery bands for the start and end images, as well as the associated valid times \(\mathbf{T}\).

Output data

A 2D field of drift vectors (\(\delta_x\) and \(\delta_y\) components) on the (n,s)h_ease2-250 grid.

A 2D field of maximum cross-correlation value for each vector.

A 2D field of status flags recording the status at the end of the CMCC optimization.

Quality Control: detect and correct outliers (“rogue” vectors)

Once the CMCC described above has been applied once to each of the start positions selected by the preliminary checks, a filtering step is taken to detect, correct or remove obviously erroneous vectors (so called “rogue” vectors).

Causes for those erroneous vectors include:

1. convergence of the Nelder Mead algorithm in a local maximum;

2. noise in the sub-images;

3. edge effects in the sub-images.

Whatever the reason be, the filtering step is based on the distance from individual displacement vectors to the average of its neighbouring vectors. If this distance is less than a fixed threshold, the displacement vector being tested is validated and another vector is tested upon. Otherwise, a new CMCC motion tracking optimisation is triggered.

In this new CMCC optimization, the Nelder Mead algorithm is initialised and run like in the previous section, except that the validity domain \(\mathbf{D}\) is adapted (center and radius) to translate the new constraint.

Erroneous vectors are detected and corrected one by one, from the “most erroneous” (see below) until all vectors are either corrected or flagged as bad.

Mathematical description

Let \(\Delta_{\textrm{avg}}\) be the distance between the tip of the current drift vector \((\delta_x,\delta_y)\) and the tip of the zonal average drift vector \((\delta^{\textrm{avg}}_x,\delta^{\textrm{avg}}_y)\). The average drift vector is computed from the 8 neighbouring drift vectors, that is the 8 closest vectors not including the current one. The local \(\mathbf{D}\) domain is then the disc with centre \((\delta^{\textrm{avg}}_x,\delta^{\textrm{avg}}_y)\) and radius \(\Delta^{\textrm{avg}}_{\textrm{max}}\). \(\Delta^{\textrm{avg}}_{\textrm{max}}\) is set to \(10\)km. Neighbouring vectors with a maximum correlation value of less than \(0.5\) are not used, to avoid degrading the average drift field with possibly wrong estimates.

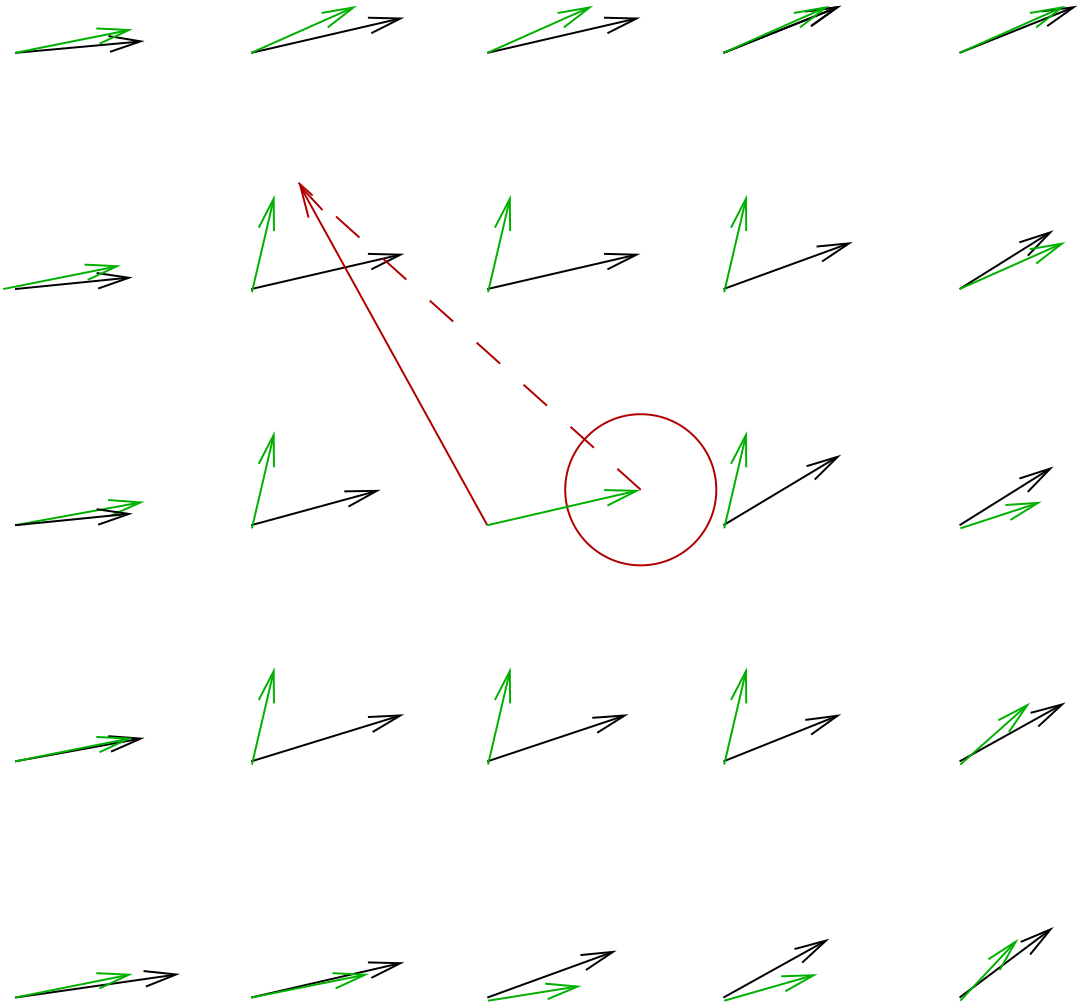
Fig. 6 Example case where the current drift vector (in red) is obviously erroneous, considered the smoother vector field from the first estimate from CMCC (in black). The locally averaged vector field is plotted in green. \(\Delta^{\textrm{avg}}\) is the length of the dashed red line. The red disc has radius \(\Delta^{\textrm{avg}}_{\textrm{max}}\) and is the validity domain $\mathbf{D} that is used to re-optimise the drift vector.

Fig. 6 illustrates a typical case where a single erroneous vector is surrounded by a smooth vector field. Since the central estimate is not used in the average, isolated wrong vectors stand out very easily in terms of their \(\Delta_{\textrm{avg}}\).

During this second CMCC optimisation, the search for the maximum is limited to the area eclosed by the red circle. If a satisfying maximum correlation is found inside \(\mathbf{D}\) it is kept and the surrounding average vectors are immediately updated, as well as each \(\Delta_{\textrm{avg}}\) lengths. If the constrained optimisation does not converge or if the new vector does not have a good enough maximum correlation value, both the old and new vectors are discarded and the average vectors, as well as \(\Delta_{\textrm{avg}}\) at the neighbouring locations are updated.

Although the method described above works in many cases, it sometimes fail when several erroneous vectors are close one to each other. This happens especially when noise dominates the signal in a large region of one of the image. If the case, the order in which the vectors are corrected has an influence on the final efficiency for the filtering.

To minimize this influence, motion vectors are first sorted from the largest to the shortest \(\Delta_{\textrm{avg}}\) and the filtering is applied to the vector exhibiting the worst of those distances. Since, changing a vector has an influence on its direct neighbours, the sorting is repeated after each correction. A mechanism is put in place to avoid falling into an infinite loop. This strategy also ensures that the good vectors around an erroneous estimate are not modified before the latter is actually processed through the filter.

In the case where the new optimization does not lead to an acceptable maximum cross-correlation value (value below the threshold, non-convergence of the CMCC with the new contraint), the vector position is recorded as non-feasible in the status flags, and the fields of drift vectors get a fill value.

This detection / correction process continues until all vectors are either corrected or flagged as non-feasible.

Input data

The 2D field of drift vectors (\(\delta_x\) and \(\delta_y\) components) on the (n,s)h_ease2-250 grid from the initial CMCC run.

The 2D field of maximum cross-correlation value for each vector from the initial CMCC run.

The 2D field of status flags recording the status at the end of the initial CMCC optimization.

Output data

Updates:

The 2D field of drift vectors (\(\delta_x\) and \(\delta_y\) components) on the (n,s)h_ease2-250 grid from the initial CMCC run.

The 2D field of maximum cross-correlation value for each vector from the initial CMCC run.

The 2D field of status flags recording the status at the end of the initial CMCC optimization.