SST Retrieval Algorithm
Contents
SST Retrieval Algorithm#
Introduction#
The retrieval algorithm is based on the regression retrieval algorithm developed in Alerskans et al., (2020). It consists of a global SST retrieval algorithm, which uses brightness temperatures and anciliary, such as wind speed. The wind speed information can be obtained from either the integrated OEM retrieval or anciliary data. In addition, an optional wind speed retriveal algorithm, based on the 2-stage retrieval algorithm developed in Alerskans et al., (2020) is included here.
As a first version, the algorithm is developed and regression coefficients are derived using data from the ESA CCI Multisensor Matchup Dataset (MMD), which includes PMW observations from AMSR2 and anciliary data from the ERA5 reanalysis. A CIMR-like channel combination is used, following Nielsen-Englyst et al., (2021), which includes the following channels; 6.9, 10.6, 18.7 and 36.5 GHz (vertical and horizontal polarizations).
Imports and parameter settings#
# Library imports
import cartopy.crs as ccrs
import datetime
import netCDF4 as nc
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
from mpl_toolkits.axes_grid1 import make_axes_locatable
import pandas as pd
import os
import scipy.io
import sklearn
from sklearn.model_selection import train_test_split
from sklearn import linear_model
import sys
# Set the random seed
rnseed = 42
# Set project paths
HOME = os.environ['HOME']
PROJECT = HOME + "/Projects/CIMR/DEVALGO/ATBD_SST"
DATA_PATH = PROJECT + "/data"
COEFF_PATH = PROJECT + "/coeffs"
# Data source and algorithm settings
channel_comb = "cimr_like" # channel combination
ws_input = "retrieval" #"retreieval": ws retrieval, "oe": consistent OEM input, "nwp": anciliary data input
data_type = "mmd"
mmd_type = "6b"
year = 2015
# Settings
Nlim = 100 # Minimum number of matchups required for robust coefficients
# Wind speed
ws_min, ws_max, dws = 0, 20, 1 # Minimum, maximum and step wind speed
ws_bins = np.arange(ws_min,ws_max,dws, dtype=int)
Read input data#
Read input data for the derivation of coefficients and subsequent retrieval of SST (and wind speed, if desired)
# Variable names
var_names = ['orbit', 'lat', 'lon', 'satza', 'sataz', 'era5_wind_dir', 'era5_phi_rel', 'era5_ws', 'era5_sst', \
'era5_tcwv', 'era5_clwt', 'tb6vpol', 'tb6hpol', 'tb10vpol', 'tb10hpol', 'tb18vpol', 'tb18hpol', \
'tb23vpol', 'tb23hpol', 'tb36vpol', 'tb36hpol', 'tb89vpol', 'tb89hpol', 'sga', 'sss', 'insitu_sst', \
'insitu_time']
# Read the data
print("Yearly file from: {}".format(year))
data_file = DATA_PATH + "/MMD" + mmd_type + "_drifter_" + str(year) + ".nc"
ncid = nc.Dataset(data_file, mode='r', format="NETCDF4_CLASSIC")
# Number of matchup
nmatchups = ncid.dimensions['matchups'].size
# Get the data
data = pd.DataFrame(index=np.arange(nmatchups))
for ivar,var_name in enumerate(var_names):
data[var_name] = ncid[var_name][:]
# Close the netCDF file
ncid.close()
# Print the first 10 rows of the dataframe to check the content
data.head(10)
Yearly file from: 2015
| orbit | lat | lon | satza | sataz | era5_wind_dir | era5_phi_rel | era5_ws | era5_sst | era5_tcwv | ... | tb23vpol | tb23hpol | tb36vpol | tb36hpol | tb89vpol | tb89hpol | sga | sss | insitu_sst | insitu_time | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 56.424183 | 169.638947 | 54.849998 | 158.089996 | 22.596886 | 135.493118 | 17.837044 | 275.812103 | 5.054865 | ... | 204.360001 | 141.500000 | 215.039993 | 156.619995 | 240.199997 | 197.949997 | 116.580383 | 32.953888 | 275.850006 | 1.420118e+09 |
| 1 | 0 | 56.424183 | 169.638947 | 54.849998 | 158.089996 | 22.297323 | 135.792679 | 17.917061 | 275.812103 | 5.006155 | ... | 204.360001 | 141.500000 | 215.039993 | 156.619995 | 240.199997 | 197.949997 | 116.580383 | 32.953888 | 275.850006 | 1.420121e+09 |
| 2 | 0 | 56.424183 | 169.638947 | 54.849998 | 158.089996 | 22.000429 | 136.089569 | 17.997564 | 275.812103 | 4.957446 | ... | 204.360001 | 141.500000 | 215.039993 | 156.619995 | 240.199997 | 197.949997 | 116.580383 | 32.953888 | 275.950012 | 1.420125e+09 |
| 3 | 0 | 56.507004 | 169.711227 | 54.849998 | 158.149994 | 21.776829 | 136.373169 | 18.030928 | 275.812103 | 4.892839 | ... | 204.429993 | 141.729996 | 215.179993 | 156.940002 | 240.350006 | 198.529999 | 116.591286 | 32.961517 | 275.950012 | 1.420129e+09 |
| 4 | 0 | 56.507004 | 169.711227 | 54.849998 | 158.149994 | 21.900801 | 136.249207 | 17.832052 | 275.812103 | 4.750621 | ... | 204.429993 | 141.729996 | 215.179993 | 156.940002 | 240.350006 | 198.529999 | 116.591286 | 32.961517 | 275.950012 | 1.420132e+09 |
| 5 | 0 | 56.507004 | 169.711227 | 54.849998 | 158.149994 | 22.027569 | 136.122437 | 17.633261 | 275.812103 | 4.608402 | ... | 204.429993 | 141.729996 | 215.179993 | 156.940002 | 240.350006 | 198.529999 | 116.591286 | 32.961517 | 275.950012 | 1.420136e+09 |
| 6 | 0 | 56.507004 | 169.711227 | 54.849998 | 158.149994 | 22.157227 | 135.992767 | 17.434559 | 275.812103 | 4.466184 | ... | 204.429993 | 141.729996 | 215.179993 | 156.940002 | 240.350006 | 198.529999 | 116.591286 | 32.961517 | 275.950012 | 1.420139e+09 |
| 7 | 0 | 29.255737 | 147.076981 | 54.840000 | 204.860001 | 133.625061 | 71.234932 | 9.008652 | 294.177734 | 11.436308 | ... | 211.240005 | 150.160004 | 214.990005 | 151.309998 | 252.539993 | 212.449997 | 135.669388 | 34.794151 | 294.250000 | 1.420114e+09 |
| 8 | 0 | 29.255737 | 147.076981 | 54.840000 | 204.860001 | 132.959351 | 71.900642 | 8.651184 | 294.177734 | 11.510617 | ... | 211.240005 | 150.160004 | 214.990005 | 151.309998 | 252.539993 | 212.449997 | 135.669388 | 34.794151 | 294.250000 | 1.420117e+09 |
| 9 | 0 | 29.255737 | 147.076981 | 54.840000 | 204.860001 | 132.236359 | 72.623634 | 8.294987 | 294.177734 | 11.584927 | ... | 211.240005 | 150.160004 | 214.990005 | 151.309998 | 252.539993 | 212.449997 | 135.669388 | 34.794151 | 294.250000 | 1.420121e+09 |
10 rows × 27 columns
Data pre-processing#
Pre-processing of data includes:
Quality control (currently only checks for NaNs as an initial QC already has been perfromed)
Definition of new variables
Splitting of the dataset into a train and test dataset
# Process the data
data['insitu_datetime'] = pd.to_datetime(data['insitu_time'],unit='s')
data['look_angle'] = data['satza'] - 55.
# Filter the data
# --Remove nans
data.dropna(axis=0,inplace=True)
# Divide the data into train and test data
data_train, data_test = train_test_split(data, test_size=0.3, random_state=rnseed)
data_train.reset_index(inplace=True)
data_test.reset_index(inplace=True)
del data
Retrieval definitions#
The main algorithm is a model for retrieving SST, which is based on the regression model developed in Alerskans et al., (2020). It uses CIMR brightness temperatures (\(T_B\)), Earth incidence angle (\(\theta_{EIA}\)), wind speed (WS) and the relative angle between wind direction and satellite azimuth angle (\(\phi_{rel}\))
where \(t_{i} = T_{Bi}-150\), \(\theta = \theta_{EIA} - 55\) and \(c_0\) - \(c_6\) are regression coefficients.
The wind speed input to the SST retrieval algorithm can come from different sources, where the main option is to use the retrieved wind speed from the integrated OEM retrieval. Optionally, anciliary wind speed data can be used. As and additional option, wind speed can be retrieved using a 2-stage retrieval algorithm based on the retrieval developed in Alerskans et al., (2020). Here, CIMR brightness temperatures and Earth incidence angle would be used to retrieved wind speed in two stages. In the first step, a global algorithm is used:
whereas in the second step, localized wind speed algorithms based on the first-step retrieved wind speed, \(WS_a\) is used to developed individual retrieval algorithms for fixed wind speed intervals:
General functions#
def regression(X,Y):
"""
Perform linear regression and obtain the regression coefficients (intercept + slope)
Arguments
---------
X: 2D float array
predictors
Y: 2D float array
predictand
Returns
-------
intercept: 1D float array
intercept
coeffs: 1D float array
slope
"""
regr = linear_model.LinearRegression()
regr.fit(X, Y)
intercept = regr.intercept_
coeffs = regr.coef_
return intercept, coeffs
def ws_algorithm_selection(data,channel_comb):
"""
Select WS algorithm based on the chosen channel combination
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
Returns
-------
X: 2D float array
algorithm input variables
"""
nmatchups = data.shape[0]
if channel_comb == 'cimr_like':
# CIMR-like configuration (based on AMSR-2 channels)
ninput = 17
X = np.full((nmatchups,ninput), fill_value=np.nan)
X[:,0] = data['tb6vpol'] - 150
X[:,1] = (data['tb6vpol'] - 150)**2
X[:,2] = data['tb6hpol'] - 150
X[:,3] = (data['tb6hpol'] - 150)**2
X[:,4] = data['tb10vpol'] - 150
X[:,5] = (data['tb10vpol'] - 150)**2
X[:,6] = data['tb10hpol'] - 150
X[:,7] = (data['tb10hpol'] - 150)**2
X[:,8] = data['tb18vpol'] - 150
X[:,9] = (data['tb18vpol'] - 150)**2
X[:,10] = data['tb18hpol'] - 150
X[:,11] = (data['tb18hpol'] - 150)**2
X[:,12] = data['tb36vpol'] - 150
X[:,13] = (data['tb36vpol'] - 150)**2
X[:,14] = data['tb36hpol'] - 150
X[:,15] = (data['tb36hpol'] - 150)**2
X[:,16] = data['look_angle']
elif channel_comb == 'cimr':
# CIMR configuration
ninput = 21
X = np.full((nmatchups,ninput), fill_value=np.nan)
X[:,0] = data['tb1vpol'] - 150
X[:,1] = (data['tb1vpol'] - 150)**2
X[:,2] = data['tb1hpol'] - 150
X[:,3] = (data['tb1hpol'] - 150)**2
X[:,4] = data['tb6vpol'] - 150
X[:,5] = (data['tb6vpol'] - 150)**2
X[:,6] = data['tb6hpol'] - 150
X[:,7] = (data['tb6hpol'] - 150)**2
X[:,8] = data['tb10vpol'] - 150
X[:,9] = (data['tb10vpol'] - 150)**2
X[:,10] = data['tb10hpol'] - 150
X[:,11] = (data['tb10hpol'] - 150)**2
X[:,12] = data['tb18vpol'] - 150
X[:,13] = (data['tb18vpol'] - 150)**2
X[:,14] = data['tb18hpol'] - 150
X[:,15] = (data['tb18hpol'] - 150)**2
X[:,16] = data['tb36vpol'] - 150
X[:,17] = (data['tb36vpol'] - 150)**2
X[:,18] = data['tb36hpol'] - 150
X[:,19] = (data['tb36hpol'] - 150)**2
X[:,20] = data['look_angle']
else:
print("Channel combination {} not understood.\nExiting...!".format(channel_comb))
sys.exit()
return X
def sst_algorithm_selection(data,channel_comb):
"""
Select SST algorithm based on the chosen channel combination
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
Returns
-------
X: 2D float array
algorithm input variables
"""
nmatchups = data.shape[0]
if channel_comb == 'cimr_like':
# CIMR-like configuration (based on AMSR-2 channels)
ninput = 22
X = np.full((nmatchups,ninput), fill_value=np.nan)
X[:,0] = data['tb6vpol'] - 150
X[:,1] = (data['tb6vpol'] - 150)**2
X[:,2] = data['tb6hpol'] - 150
X[:,3] = (data['tb6hpol'] - 150)**2
X[:,4] = data['tb10vpol'] - 150
X[:,5] = (data['tb10vpol'] - 150)**2
X[:,6] = data['tb10hpol'] - 150
X[:,7] = (data['tb10hpol'] - 150)**2
X[:,8] = data['tb18vpol'] - 150
X[:,9] = (data['tb18vpol'] - 150)**2
X[:,10] = data['tb18hpol'] - 150
X[:,11] = (data['tb18hpol'] - 150)**2
X[:,12] = data['tb36vpol'] - 150
X[:,13] = (data['tb36vpol'] - 150)**2
X[:,14] = data['tb36hpol'] - 150
X[:,15] = (data['tb36hpol'] - 150)**2
X[:,16] = data['look_angle']
X[:,17] = data['WSr']
X[:,18] = np.cos(data['era5_phi_rel'])
X[:,19] = np.sin(data['era5_phi_rel'])
X[:,20] = np.cos(2*data['era5_phi_rel'])
X[:,21] = np.sin(2*data['era5_phi_rel'])
elif channel_comb == 'cimr_like_simple':
# CIMR-like configuration (based on AMSR-2 channels),
# using only brighness temperature
ninput = 16
X = np.full((nmatchups,ninput), fill_value=np.nan)
X[:,0] = data['tb6vpol'] - 150
X[:,1] = (data['tb6vpol'] - 150)**2
X[:,2] = data['tb6hpol'] - 150
X[:,3] = (data['tb6hpol'] - 150)**2
X[:,4] = data['tb10vpol'] - 150
X[:,5] = (data['tb10vpol'] - 150)**2
X[:,6] = data['tb10hpol'] - 150
X[:,7] = (data['tb10hpol'] - 150)**2
X[:,8] = data['tb18vpol'] - 150
X[:,9] = (data['tb18vpol'] - 150)**2
X[:,10] = data['tb18hpol'] - 150
X[:,11] = (data['tb18hpol'] - 150)**2
X[:,12] = data['tb36vpol'] - 150
X[:,13] = (data['tb36vpol'] - 150)**2
X[:,14] = data['tb36hpol'] - 150
X[:,15] = (data['tb36hpol'] - 150)**2
elif channel_comb == 'cimr':
# CIMR configuration
ninput = 26
X = np.full((nmatchups,ninput), fill_value=np.nan)
X[:,0] = data['tb1vpol'] - 150
X[:,1] = (data['tb1vpol'] - 150)**2
X[:,2] = data['tb1hpol'] - 150
X[:,3] = (data['tb1hpol'] - 150)**2
X[:,4] = data['tb6vpol'] - 150
X[:,5] = (data['tb6vpol'] - 150)**2
X[:,6] = data['tb6hpol'] - 150
X[:,7] = (data['tb6hpol'] - 150)**2
X[:,8] = data['tb10vpol'] - 150
X[:,9] = (data['tb10vpol'] - 150)**2
X[:,10] = data['tb10hpol'] - 150
X[:,11] = (data['tb10hpol'] - 150)**2
X[:,12] = data['tb18vpol'] - 150
X[:,13] = (data['tb18vpol'] - 150)**2
X[:,14] = data['tb18hpol'] - 150
X[:,15] = (data['tb18hpol'] - 150)**2
X[:,16] = data['tb36vpol'] - 150
X[:,17] = (data['tb36vpol'] - 150)**2
X[:,18] = data['tb36hpol'] - 150
X[:,19] = (data['tb36hpol'] - 150)**2
X[:,20] = data['look_angle']
X[:,21] = data['WSr']
X[:,22] = np.cos(data['era5_phi_rel'])
X[:,23] = np.sin(data['era5_phi_rel'])
X[:,24] = np.cos(2*data['era5_phi_rel'])
X[:,25] = np.sin(2*data['era5_phi_rel'])
else:
print("Channel combination {} not understood.\nExiting...!".format(channel_comb))
sys.exit()
return X
def calculate_coeffs_ws(data,channel_comb):
"""
Perform regression of wind speed
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
Returns
-------
coeffs_all: 1D float array
regression coefficients
"""
# Predictors
X = ws_algorithm_selection(data,channel_comb)
# Predictand
Y = data['era5_ws'].values
# the try...continue structure is to account for cases where we
# don't have data in a particular bin, then the code moves on
try:
# Calculate linear regression coefficients
intercept, coeffs = regression(X,Y)
coeffs_all = np.append(intercept,coeffs)
return coeffs_all
except:
return np.full((ninput+1), fill_value=np.nan)
def calculate_coeffs_sst(data,channel_comb):
"""
Perform regression of SST
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
Returns
-------
coeffs_all: 1D float array
regression coefficients
"""
# Predictors
X = sst_algorithm_selection(data,channel_comb)
# Predictand
Y = data['insitu_sst'].values
# the try...continue structure is to account for cases where we
# don't have data in a particular bin, then the code moves on
try:
# Calculate linear regression coefficients
intercept, coeffs = regression(X,Y)
coeffs_all = np.append(intercept,coeffs)
return coeffs_all
except:
return np.full((ninput+1), fill_value=np.nan)
def retrieve_ws(data,A,channel_comb):
"""
Perform WS retrieval
Arguments
---------
data: pandas DataFrame
dataset
A: 1D float array
regression coefficients
channel_comb: str
choice of channel combination
Returns
-------
WS: 1D float array
retirved wind speed
"""
# Settings
nmatchups = data.shape[0]
# Predictors
X = ws_algorithm_selection(data,channel_comb)
# Add input for the offset/intercept
X = np.hstack((np.ones((nmatchups,1)),X))
# Retrieve WS
WS = np.dot(A,X.T)
return WS
def retrieve_sst(data,A,channel_comb):
"""
Perform SST retrieval
Arguments
---------
data: pandas DataFrame
dataset
A: 1D float array
regression coefficients
channel_comb: str
choice of channel combination
Returns
-------
SST: 1D float array
retirved SST
"""
# Settings
nmatchups = data.shape[0]
# Predictors
X = sst_algorithm_selection(data,channel_comb)
# Add input for the offset/intercept
X = np.hstack((np.ones((nmatchups,1)),X))
# Retrieve SST
SST = np.dot(A,X.T)
return SST
Stage 1 wind speed retrieval algorithm#
Derivation of 1st-stage wind speed regression coefficients
Retrieval of 1st-stage wind speed
def calculate_coeffs_stage_1_ws(data,channel_comb,verbose=False):
"""
Derivation of stage 1 wind speed regression coefficients.
Global coefficients (i.e. based on the whole dataset) is derived.
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice fo channel combination
verbose: logical
logical for verbosity of function
Returns
-------
"""
print("\nCalculate WS stage 1 coefficients")
# Get coefficients
coeffs_all = calculate_coeffs_ws(data,channel_comb)
if not np.all(np.isnan(coeffs_all)):
if verbose:
print("Save WS stage 1 coefficients")
coeffs_file = "{}/ws/coeffs_{}_ws_stage_1.npy".format(COEFF_PATH,channel_comb)
np.save(coeffs_file,coeffs_all)
def retrieve_stage_1_ws(data,channel_comb):
"""
Retrieval of global stage 1 wind speeds.
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
Returns
-------
WSa: 1D float array
retrieved wind speed
"""
print("\nRetrieve stage 1 WS")
# Load coefficients
coeffs_file = "{}/ws/coeffs_{}_ws_stage_1.npy".format(COEFF_PATH,channel_comb)
A = np.load(coeffs_file)
# Retrieve WS
WSa = retrieve_ws(data,A,channel_comb)
return WSa
Stage 2 wind speed retrieval algorithm#
Derivation of 2nd-stage wind speed regression coefficients
Retrieval of 2nd-stage wind speed
def calculate_coeffs_stage_2_ws(data,ws_bins,channel_comb,verbose=False):
"""
Derivation of stage 2 wind speed regression coefficients.
Localized coeffients for specified wind speed intervals are derived.
The wind speed intervals are based on the 1st-stage retrieved wind speed.
Arguments
---------
data: pandas DataFrame
dataset
ws_bins: 1D float array
wind speed bin intervals
channel_comb: str
choice of channel combination
verbose: logical
logical for verbosity of function
Returns
-------
"""
print("\nCalculate WS stage 2 coefficients")
# Settings
ws_step = ws_bins[1] - ws_bins[0]
# Loop through bins
for iws in ws_bins:
# Find the data that belongs to the current wind speed bin
mask_sub = ( (data['WSa'].values > iws) & (data['WSa'].values <= iws+ws_step) )
# Check so that there is enough data
if np.sum(mask_sub) > Nlim:
data_sub = data.loc[mask_sub]
# Calculate coefficients
coeffs_all = calculate_coeffs_ws(data_sub,channel_comb)
if not np.all(np.isnan(coeffs_all)):
if verbose:
print("Save WS stage 2 coefficients for wind speed bin {}-{} ms-1".format(iws,iws+1))
coeffs_file = "{}/ws/coeffs_{}_ws_stage_2_wsbin_{:02d}.npy".format(COEFF_PATH,channel_comb,iws)
np.save(coeffs_file,coeffs_all)
def retrieve_stage_2_ws(data,ws_bins,channel_comb,verbose=False):
"""
Retrieval of local stage 2 wind speeds.
Arguments
---------
data: pandas DataFrame
dataset
ws_bins: 1D float array
wind speed bins for localized algoritm
channel_comb: str
choice of channel combination
Returns
-------
WSr: 1D float array
retrieved wind speed
"""
print("\nRetrieve stage 2 WS")
# Settings
nmatchups = data.shape[0]
ws_step = ws_bins[1] - ws_bins[0]
# Initialize array
WSr = np.full((nmatchups), fill_value=np.nan, dtype=np.float32)
# Loop through bins
for iws in ws_bins:
if verbose:
print("Working on wind speed bin {}".format(iws))
# Find the data that belongs to the current wind speed bin
mask_sub = (data['WSa'].values > iws) & (data['WSa'].values <= iws+ws_step)
# Check so that there is data
if np.sum(mask_sub) > 0:
idx_sub = np.argwhere(mask_sub)[:,0]
data_sub = data.loc[mask_sub]
data_sub.reset_index(inplace=True,drop=True)
# Load the appropriate coefficient file
coeffs_file = "{}/ws/coeffs_{}_ws_stage_2_wsbin_{:02d}.npy".format(COEFF_PATH,channel_comb,iws)
if os.path.isfile(coeffs_file):
B1 = np.load(coeffs_file)
isnan_B1 = False
else:
isnan_B1 = True
# If interpolating, find the nearest wind speed bin of our measurement
for inear in range(2):
if inear == 0:
# Lower limit
iws_near = iws - ws_step
mask_int = (data_sub['WSa'].values < iws + ws_step/2)
if np.sum(mask_int) == 0:
continue
idx_int = np.argwhere(mask_int)[:,0]
data_int = data_sub.loc[mask_int]
else:
# Upper limit
iws_near = iws + ws_step
mask_int = (data_sub['WSa'].values >= iws + ws_step/2)
if np.sum(mask_int) == 0:
continue
idx_int = np.argwhere(mask_int)[:,0]
data_int = data_sub.loc[mask_int]
# Check if there are coefficients for that bin and load
coeffs_file_near = "{}/ws/coeffs_{}_ws_stage_2_wsbin_{:02d}.npy".format(COEFF_PATH,channel_comb,iws_near)
if os.path.isfile(coeffs_file_near):
B2 = np.load(coeffs_file_near)
isnan_B2 = False
elif os.path.isfile(coeffs_file):
isnan_B2 = True
B2 = B1.copy()
else:
# No coefficients for current or closest ws bin -> no retrieval
if verbose:
print("Warning: Coefficients do not exist for current wind speed bin {} or closest bin. WS=NaN...!".format(iws))
WSr[idx_sub[idx_int]] = np.nan
continue
# Retrieve WS
WSr_i1 = retrieve_ws(data_int,B1,channel_comb)
WSr_i2 = retrieve_ws(data_int,B2,channel_comb)
# Define interpolation weights
w1 = np.abs(data_int['WSa'].values - iws)/ws_step
w2 = 1 - w1
# Reset weights as we don't have either B1 or B2 coefficients
if (isnan_B1 | isnan_B2):
if (isnan_B1): w1 = 0.
if (isnan_B2): w2 = 0.
wsum = w1 + w2
w1 = w1 / wsum
w2 = w2 / wsum
# Interpolate between WSr_i1 and WSr_i2
WSr_int = WSr_i1 * w1 + WSr_i2 * w2
# Assign to the correct WSr elements
WSr[idx_sub[idx_int]] = WSr_int.copy()
return WSr
SST retrieval algorithm#
Derivation of SST regression coefficients
Retrieval of SST
def calculate_coeffs_global_sst(data,channel_comb,verbose=False):
"""
Derivation of SST coefficients.
Global coeffients (i.e. based on the whole dataset) are derived.
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
verbose: logical
logical for verbosity of function
Returns
-------
"""
print("\nCalculate SST global coefficients")
# Exclude WSr nans
data_sub = data.dropna(axis=0)
# Get coefficients
coeffs_all = calculate_coeffs_sst(data_sub,channel_comb)
if not np.all(np.isnan(coeffs_all)):
if verbose:
print("Save SST global coefficients")
coeffs_file = "{}/sst/coeffs_{}_sst_global.npy".format(COEFF_PATH,channel_comb)
np.save(coeffs_file,coeffs_all)
def retrieve_global_sst(data,channel_comb):
"""
Retrieval of global SSTs.
Arguments
---------
data: pandas DataFrame
dataset
channel_comb: str
choice of channel combination
Returns
-------
SSTr: 1D float array
retrieved SST
"""
print("\nRetrieve global SST")
# Load coefficients
coeffs_file = "{}/sst/coeffs_{}_sst_global.npy".format(COEFF_PATH,channel_comb)
A = np.load(coeffs_file)
# Retrieve SST
SSTr = retrieve_sst(data,A,channel_comb)
return SSTr
Derivation of regression coefficients#
Here, regression coefficients for the SST retrieval algorithm is derived. In addition, if the option is set to use retrieved wind speed in the SST algorithm, the 1st- and 2nd-stage wind speed coefficients are retrieved here as well.
# Settings
derive_stage_1_ws_coeffs = True
derive_stage_2_ws_coeffs = True
derive_global_sst_coeffs = True
if ws_input == "retrieval":
# ------------------------------
# Wind speed retrieval - Stage 1
# ------------------------------
# Calculate coefficients
if derive_stage_1_ws_coeffs:
calculate_coeffs_stage_1_ws(data_train,channel_comb)
# Retrieve WSa
WSa = retrieve_stage_1_ws(data_train,channel_comb)
data_train['WSa'] = WSa
if ws_input == "retrieval":
# ------------------------------
# Wind speed retrieval - Stage 2
# ------------------------------
# Calculate coefficients
if derive_stage_2_ws_coeffs:
calculate_coeffs_stage_2_ws(data_train,ws_bins,channel_comb)
# Retrieve WSr
WSr = retrieve_stage_2_ws(data_train,ws_bins,channel_comb)
data_train['WSr'] = WSr
elif ws_input == "oe":
# Input from the integrated OEM retrieval - not implemented yet
pass
elif ws_input == "nwp":
# Input from NWP ERA5 data
data_train['WSr'] = data_train['era5_ws']
# -----------------------
# SST retrieval - Global
# -----------------------
# Calculate coefficients
if derive_global_sst_coeffs:
calculate_coeffs_global_sst(data_train,channel_comb)
# Retrieve SSTr
SSTr = retrieve_global_sst(data_train,channel_comb)
data_train['SSTr_global'] = SSTr
print("...Done!")
Calculate WS stage 1 coefficients
Retrieve stage 1 WS
Calculate WS stage 2 coefficients
Retrieve stage 2 WS
Calculate SST global coefficients
Retrieve global SST
...Done!
Performance analysis#
Use the test dataset to retrieve SST and evaluate the performance of the retrieval algorithm.
Analysis functions#
Define functions used for evaluating the performance of the algorithm.
def print_stats(data,SSTr):
"""
Print the overall perfromance metrics for the SST retrieval algorithm.
Arguments
---------
data: pandas DataFrame
dataset
SSTr: 1D float array
retrieved SST
Returns
-------
Prints output
"""
dif_mean = np.nanmean(SSTr - data['insitu_sst'])
dif_mae = np.nanmean(np.abs(SSTr - data['insitu_sst']))
dif_std = np.nanstd(SSTr - data['insitu_sst'])
dif_rmse = np.sqrt(np.nanmean((SSTr - data['insitu_sst'])**2))
print('PMW retrievals - drifter observations')
print('-------------------------------------')
print('Mean: ' + str(round(dif_mean,3)) + ' K.')
print('MAE: ' + str(round(dif_mae,3)) + ' K.')
print('St.d: ' + str(round(dif_std,3)) + ' K.')
print('RMSE: ' + str(round(dif_rmse,3)) + ' K.')
def plot_scatter_data(data,pmin_sst,pmax_sst,pdsst):
"""
Scatterplot of retrieved SST (y-axis) vs. drifter in situ SST (x-axis).
Arguments
---------
data: pandas DataFrame
dataset
pmin_sst: float
SST min (x- and y-min) limits for plot
pmax_sst: float
SST max (x- and y-max) limits for plot
Returns
-------
Outputs a figure
"""
fig, ax = plt.subplots(figsize=[8,6])
ax.scatter(data['insitu_sst']-273.15,data['SSTr_global']-273.15)
ax.plot([pmin_sst,pmax_sst],[pmin_sst,pmax_sst], linestyle='-', color='k', linewidth=1.2)
ax.grid(True)
ax.set_xlabel('in situ SST ($^{\circ}$C)',fontsize=13)
ax.set_ylabel('retrieved PMW SST ($^{\circ}$C)',fontsize=13)
ax.set_xlim([pmin_sst, pmax_sst])
ax.set_ylim([pmin_sst, pmax_sst])
ax.set_xticks(np.arange(pmin_sst,pmax_sst+pdsst,pdsst))
ax.set_yticks(np.arange(pmin_sst,pmax_sst+pdsst,pdsst))
ax.set_xticklabels(np.arange(pmin_sst,pmax_sst+pdsst,pdsst),fontsize=12)
ax.set_yticklabels(np.arange(pmin_sst,pmax_sst+pdsst,pdsst),fontsize=12)
plt.show()
def gridded_statistics(lat,lon,y,Nmin,grid_size,verbose=False):
"""
Function for calculating statistics and the number of matchups in each latitude grid cell.
Arguments
---------
lat: 1D float array
In situ latitude
lon: 1D float array
In situ longitude
Nmin: int
Minimum number of matchuos required to calculate statistics in a grid cell
grid_size: int
Size of the grid
verbose: logical
Logical for verbosity of function
Returns
-------
lat_grid: 2D float array
Gridded latitudes
lon_grid: 2D float array
Gridded longitudes
stat: 2D structured array
Gridded statistics (N, mean, std, RMSE)
"""
# Read in the land/sea/ice mask (matlab file)
maskfile = DATA_PATH + '/Land_Ice_Water_Mask_dgrid_' + str(grid_size) + '.mat'
# Use scipy.io.loadmat to load the file
data_dict = scipy.io.loadmat(maskfile)
land_sea_ice_mask = data_dict['water_mask']
lat_grid = data_dict['latm']
lon_grid = data_dict['lonm']
Nlat = int(data_dict['Nlat'])
Nlon = int(data_dict['Nlon'])
# Create structured data type
var_names = ['N', 'mean', 'std', 'rmse']
var_types = ['f8', 'f8', 'f8', 'f8']
array_type_list = []
for i in range(len(var_names)):
array_type_list.append((var_names[i],var_types[i]))
# Initialize structured array
stat = np.zeros((Nlat,Nlon),dtype=array_type_list)
stat['N'][:,:] = np.nan
stat['mean'][:,:] = np.nan
stat['std'][:,:] = np.nan
stat['rmse'][:,:] = np.nan
print('Calculate the gridded statistics: ' + str(grid_size) + 'x' + str(grid_size))
for i in range(Nlon):
for j in range(Nlat):
if verbose:
print('Calculating statistics. Longitude: ' + str(i) + ' Latitude: ' + str(j))
if (land_sea_ice_mask[i,j] > 0):
mask = ( (lat < (lat_grid[i,j] + grid_size/2) ) & \
(lat >= (lat_grid[i,j] - grid_size/2) ) & \
(lon < (lon_grid[i,j] + grid_size/2) ) & \
(lon >= (lon_grid[i,j] - grid_size/2) ) )
# Check if wwe have enough matchups
if ( np.sum(mask == True) > Nmin ):
stat['N'][j,i] = int(np.sum(mask == True))
stat['mean'][j,i] = np.nanmean(y[mask])
stat['std'][j,i] = np.nanstd(y[mask])
stat['rmse'][j,i] = np.sqrt(np.nanmean(y[mask]**2))
return lat_grid, lon_grid, stat
def plot_gridded_statistics(lat_grid,lon_grid,stat,parameters):
"""
Funciton for plotting gridded statistics:
+ No. of matchups, N
+ Mean Error
+ Standard deviation
+ RMSE
Arguments
---------
lat_grid: 2D float array
Gridded latitudes
lon_grid: 2D float array
Gridded longitudes
stat: 2D structured array
Gridded statistics (N, mean, std, RMSE)
parameters: dictionary
Dictionary with plot options
Returns
-------
[figure]
"""
# Read values form dictionary
cb_min = parameters['cb_min']
cb_max = parameters['cb_max']
cb_step = parameters['cb_step']
# Plot settings
Lon_max = 180.
Lon_min = -180.
Lon_step = 60
Lat_max = 90.
Lat_min = -90.
Lat_step = 30
stat_vars = ['N', 'mean', 'std', 'rmse'] # Statistics variables
cmap_type = [plt.cm.viridis,plt.cm.seismic,plt.cm.YlOrRd,plt.cm.YlOrRd]
cb_labels = ['No. of matchups','Mean difference ($^{\circ}$C)','Standard deviation ($^{\circ}$C)','RMSE ($^{\circ}$C)']
cb_ticks = [np.arange(cb_min[0], cb_max[0]+cb_step[0], cb_step[0]), \
np.arange(cb_min[1], cb_max[1]+cb_step[1], cb_step[1]), \
np.arange(cb_min[2], cb_max[2]+cb_step[2], cb_step[2]), \
np.arange(cb_min[3], cb_max[3]+cb_step[3], cb_step[3])]
for i,stat_var in enumerate(stat_vars):
#fig, ax = plt.subplots(figsize=[14, 7], projection=ccrs.PlateCarree())
fig = plt.figure(figsize=[14,7])
ax = fig.add_subplot(1,1,1, projection=ccrs.PlateCarree())
im = ax.pcolormesh(lon_grid,lat_grid,stat[stat_var].T, transform=ccrs.PlateCarree(),
cmap=cmap_type[i], vmin=cb_min[i], vmax=cb_max[i])#,latlon=True)
ax.coastlines()
ax.set_extent([Lon_min, Lon_max, Lat_min, Lat_max])
gl = ax.gridlines(crs=ccrs.PlateCarree(), draw_labels=True, linewidth=1, color='k', alpha=0.5, linestyle=':')
gl.top_labels = False
gl.right_labels = False
gl.xlocator = mticker.FixedLocator(np.arange(Lon_min,Lon_max+Lon_step,Lon_step))
gl.ylocator = mticker.FixedLocator(np.arange(Lat_min,Lat_max+Lon_step,Lat_step))
gl.xlabel_style = {'size': 14}
gl.ylabel_style = {'size': 14}
# Colorbar
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="3%", pad="2%", axes_class=plt.Axes)
cb = fig.colorbar(im, cax=cax)
cb.set_label(label=cb_labels[i], fontsize=16, labelpad=20.0)
cb.ax.set_ylim(cb_min[i], cb_max[i])
cb.ax.set_yticks(cb_ticks[i])
cb.ax.tick_params(labelsize=14)
plt.show()
Retrieval of SST#
Retrieve wind speed (if this option is set) and SST
# WS data
if ws_input == "retrieval":
# Retrieve WSa
WSa = retrieve_stage_1_ws(data_test,channel_comb)
data_test['WSa'] = WSa
# Retrieve WSr
WSr = retrieve_stage_2_ws(data_test,ws_bins,channel_comb)
data_test['WSr'] = WSr
elif ws_input == "oe":
# Not implemented yet
pass
elif ws_input == "nwp":
print("ERA5 WS input")
data_test['WSr'] = data_test['era5_ws']
# Retrieve SSTr
SSTr = retrieve_global_sst(data_test,channel_comb)
data_test['SSTr_global'] = SSTr
print("...Done!")
Retrieve stage 1 WS
Retrieve stage 2 WS
Retrieve global SST
...Done!
# Only use the common data, i.e. remove any NaNs
good_data = ( ~np.isnan(data_test['SSTr_global'].values) )
data_test = data_test.loc[good_data,:]
data_test.reset_index(inplace=True,drop=True)
Overall performance#
The overall performance of the SST retrieval algorithm for the test dataset, with respect to mean difference/bias, mean absolute error (MAE), standard deviation (st.d) and root mean square error (RMSE) is shown below .
print("\nTEST DATASET - Global SST retrieval")
print("======================================")
print_stats(data_test,data_test['SSTr_global'])
TEST DATASET - Global SST retrieval
======================================
PMW retrievals - drifter observations
-------------------------------------
Mean: 0.0 K.
MAE: 0.552 K.
St.d: 0.745 K.
RMSE: 0.745 K.
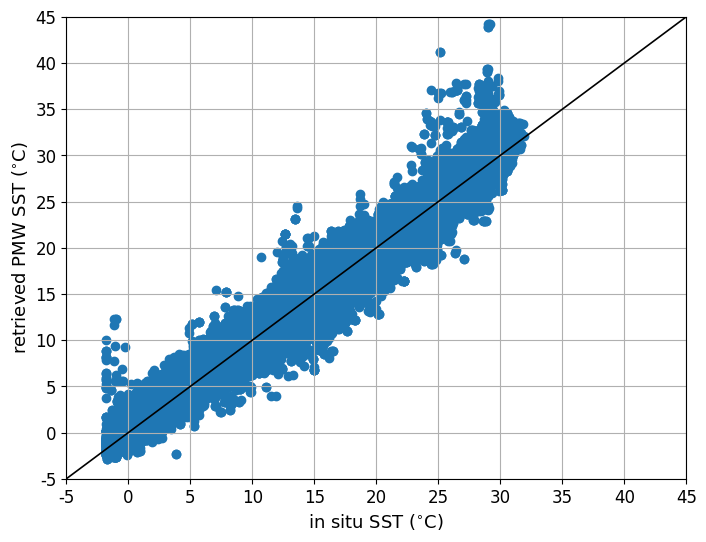
Scatter plot results#
The retrieved PMW SST is plotted against the drifter in situ SST.
# Plot scatter plot of retrieved vs in situ SST
pmin_sst = -5
pmax_sst = 45
pdsst = 5
plot_scatter_data(data_test,pmin_sst,pmax_sst,pdsst)
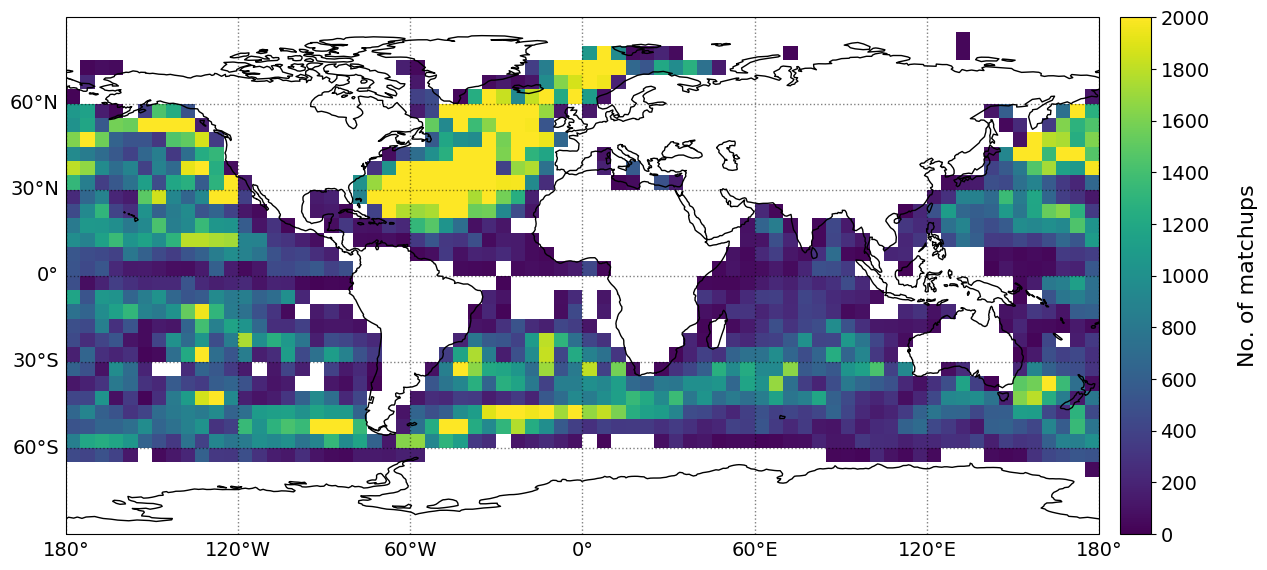
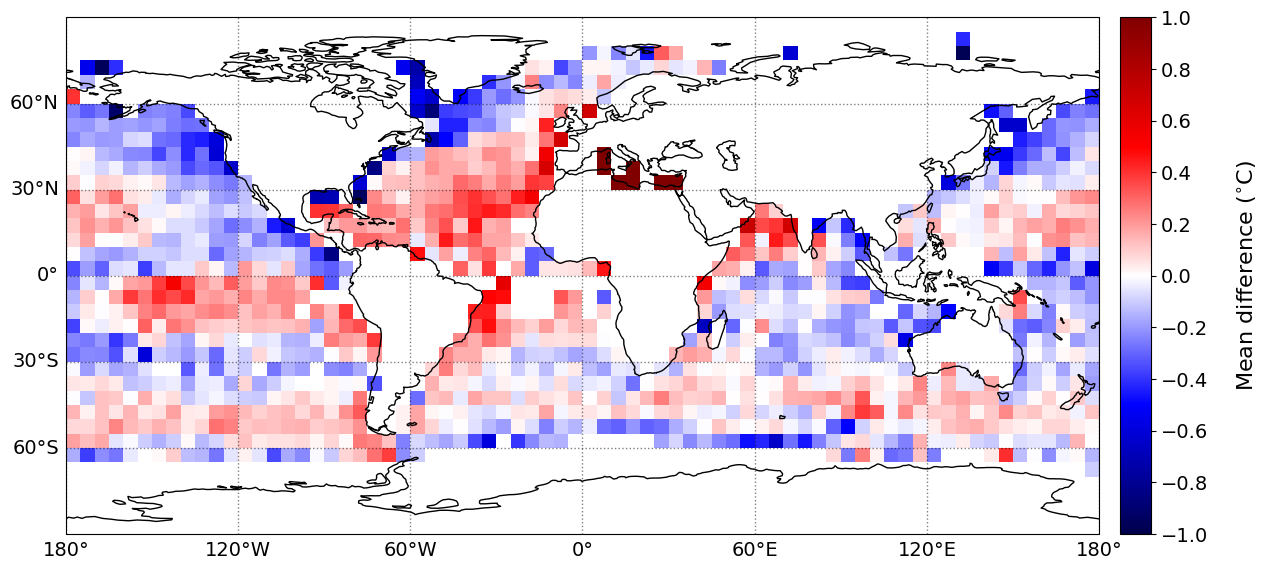
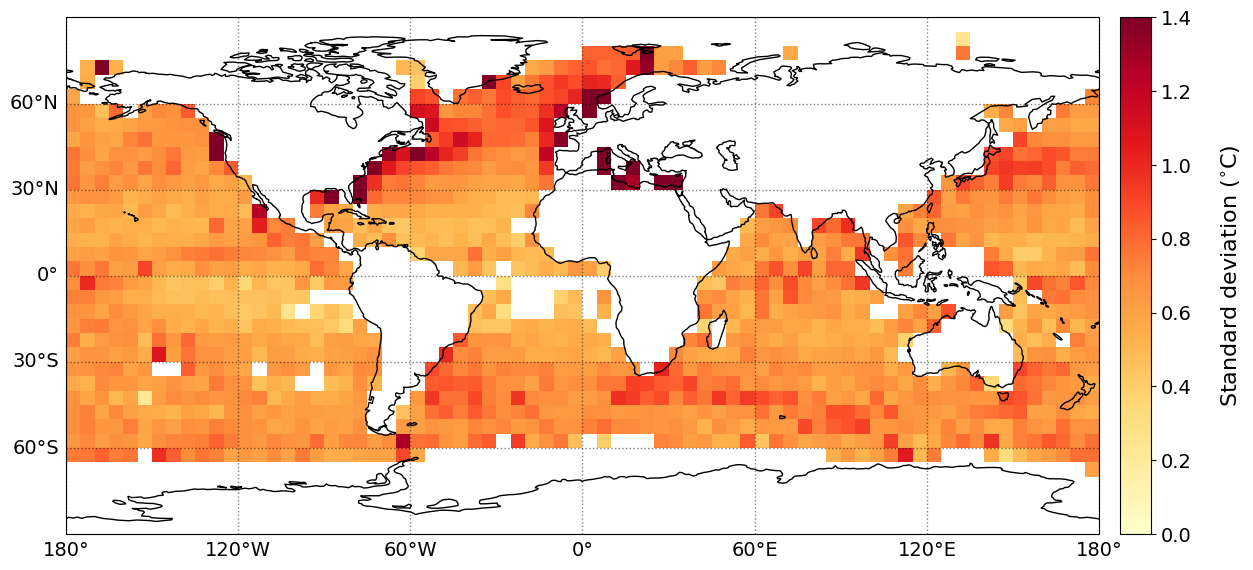
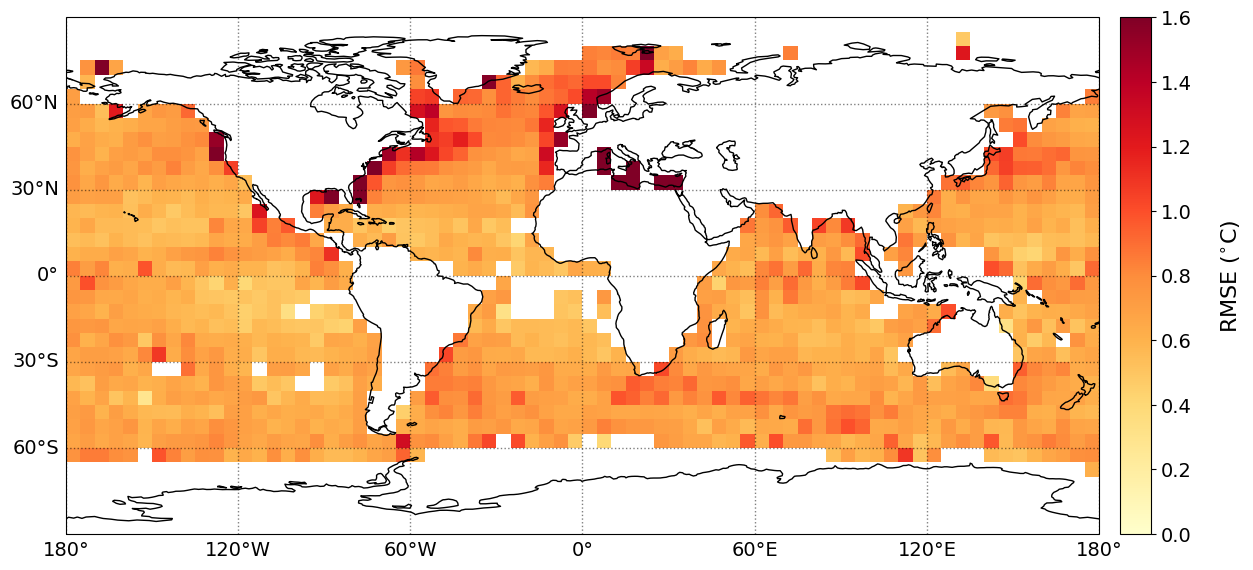
Gridded statistics#
The geographical distribution of mean difference/bias, MAE, Std. and RMSE of the SST bias (retrieved PMW SST minus in situ SST) are shown below. The statistics have been gridded using a grid size of 5\(^{\circ}\), with a minimum of 20 matchups per grid cell.
# Calculate gridded statistics
Nmin = 20
grid_size = 5
y = data_test['insitu_sst'].values - data_test['SSTr_global'].values
lon = data_test['lon'].values
lat = data_test['lat'].values
lat_grid, lon_grid, stat = gridded_statistics(lat,lon,y,Nmin,grid_size,verbose=False)
Calculate the gridded statistics: 5x5
# Plot the gridded statistics
plot_parameters = {}
plot_parameters['cb_min'] = [0, -1., 0., 0] # Minimum value on colorbar
plot_parameters['cb_max'] = [2000, 1., 1.4, 1.6] # Maximum value on colorbar
plot_parameters['cb_step'] = [200, 0.2, 0.2, 0.2] # Step value on colorbar
plot_gridded_statistics(lat_grid,lon_grid,stat,plot_parameters)